#include <Util_Minimization_Methods.hpp>
Public Member Functions | |
| Minimizer (DFLib::Abstract::Group *aGroup) | |
| void | bracketMinimum (double &a, double &b, double &c, std::vector< double > &X0, std::vector< double > &direction) |
| bracket minimum of function | |
| double | brentMinimize (double a, double b, double c, std::vector< double > &X0, std::vector< double > &direction, double &xmin) |
| minimize by Brent's method with derivatives given a,b,c scalars that bracket the minimum in given direction from X0, search for minimum using Brent's method Returns function value, sets "xmin" to abscissa at minimum. Almost verbatim port out of Numerical Recipes in C | |
| double | lineSearch (std::vector< double > &X0, std::vector< double > &dir) |
| minimize function in given direction perform a line search along the given direction for the minimum value of the function. | |
| double | conjugateGradientMinimize (std::vector< double > &X0, double ftol, int &iter) |
| minimize function of vector value by method of conjugate gradients | |
| int | nelderMeadMinimize (std::vector< std::vector< double > > &Simplex) |
| minimuze function of vector argument by Nelder-Mead simplex method. | |
| double | simpleF (double &x, std::vector< double > &X0, std::vector< double > &dir) |
| Evaluate | |
| double | simpleFandDeriv (double &x, std::vector< double > &X0, std::vector< double > &dir, double &df) |
Private Attributes | |
| DFLib::Abstract::Group * | theGroup |
Constructor & Destructor Documentation
◆ Minimizer()
|
inline |
Member Function Documentation
◆ bracketMinimum()
| void DFLib::Util::Minimizer::bracketMinimum | ( | double & | a, |
| double & | b, | ||
| double & | c, | ||
| std::vector< double > & | X0, | ||
| std::vector< double > & | direction | ||
| ) |
bracket minimum of function
Given scalars 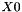
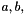
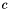
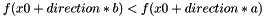
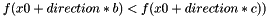
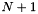


◆ brentMinimize()
| double DFLib::Util::Minimizer::brentMinimize | ( | double | a, |
| double | b, | ||
| double | c, | ||
| std::vector< double > & | X0, | ||
| std::vector< double > & | direction, | ||
| double & | xmin | ||
| ) |
minimize by Brent's method with derivatives given a,b,c scalars that bracket the minimum in given direction from X0, search for minimum using Brent's method Returns function value, sets "xmin" to abscissa at minimum. Almost verbatim port out of Numerical Recipes in C


◆ conjugateGradientMinimize()
| double DFLib::Util::Minimizer::conjugateGradientMinimize | ( | std::vector< double > & | X0, |
| double | ftol, | ||
| int & | iter | ||
| ) |
minimize function of vector value by method of conjugate gradients
- Parameters
-
X0 on input starting point, on exit solution. ftol convergence tolerance on function. iter returned number of iterations taken
- Returns
- value of function at minimum.


◆ lineSearch()
| double DFLib::Util::Minimizer::lineSearch | ( | std::vector< double > & | X0, |
| std::vector< double > & | dir | ||
| ) |
minimize function in given direction perform a line search along the given direction for the minimum value of the function.
- Parameters
-
X0 input: starting point output: minimum point dir input: direction to search output: actual displacement
- Returns
- function value at minimum. Nearly verbatim port out of Numerical Recipes in C


◆ nelderMeadMinimize()
| int DFLib::Util::Minimizer::nelderMeadMinimize | ( | std::vector< std::vector< double > > & | Simplex | ) |
minimuze function of vector argument by Nelder-Mead simplex method.
- Parameters
-
Simplex vector of vector of points representing simplex vertices
- Returns
- index into modified simplex of vertex with lowest function value
The Nelder-Mead simplex method is a minimization method in which a "simplex" is morphed through the landscape of the function and tends downhill. In 2-D the simplex is a triangle, in 3-D a tetrahedron, and in more dimensions it is a generalization of such a shape. In 
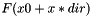
Centroid point: the centroid of the side opposite the worst point.
Reflected point: The reflection of the worst point through the centroid.
Expanded point: a point extrapolated along the line from the centroid to the reflected point at twice the distance.
Contracted point: a point halfway between the centroid and the worst point.
Reduced simplex: the simplex shrunk by half along all sides, leaving the best point unmodified.
The method improves the simplex by the following algorithm:
if the reflected point is the best so far, try the expanded point If the expanded point is the best so far, replace the worst point with it. Otherwise replace the worst point with the reflected point.
If the reflected point is not the best so far, but is better than the second-worst, replace the worst point with it.
If we haven't replaed the worst point yet, check the contracted point. If it is better than the second-worst point, replace the worst point with it.
If nothing has worked so far, reduce the size of the simplex by shrinking along all sides towards the current best point.
The method stops when we have either exceeded the maximum number of function evaluations (here hard-coded to 5000) or the spread of values between best and worst has been reduced to a sufficiently small fraction of the average of best and worst.
The stopping criterion is (abs(diff)/average)<sqrt(machine_epsilon)


◆ simpleF()
| double DFLib::Util::Minimizer::simpleF | ( | double & | x, |
| std::vector< double > & | X0, | ||
| std::vector< double > & | dir | ||
| ) |
Evaluate 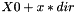
F is the group's function "computeFunctionValue"
- Returns
- function value at
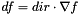


◆ simpleFandDeriv()
| double DFLib::Util::Minimizer::simpleFandDeriv | ( | double & | x, |
| std::vector< double > & | X0, | ||
| std::vector< double > & | dir, | ||
| double & | df | ||
| ) |
Evaluate F(x0+x*dir) and its directional derivative where x0 and dir are vectors. The directional derivative is the inner product of the gradient and the direction: 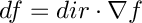


Member Data Documentation
◆ theGroup
|
private |
The documentation for this class was generated from the following files:
- /users/russo/DFLIB_Git/DFLib/Util_Minimization_Methods.hpp
- /users/russo/DFLIB_Git/DFLib/Util_Minimization_Methods.cpp