#include <DF_Report_Collection.hpp>
Public Member Functions | |
| ReportCollection () | |
| virtual | ~ReportCollection () |
| DF Report Collection destructor. | |
| virtual void | deleteReports () |
| destroy all reports stored in collection | |
| virtual int | addReport (DFLib::Abstract::Report *aReport) |
| Add a DF report to the collection. | |
| bool | computeFixCutAverage (DFLib::Abstract::Point &FCA, std::vector< double > &FCA_stddev, double minAngle=0) |
| return the fix cut average of this collection's reports | |
| void | computeLeastSquaresFix (DFLib::Abstract::Point &LS_Fix) |
| Computes least squares solution of DF problem. | |
| void | computeStansfieldFix (DFLib::Abstract::Point &SFix, double &am2, double &bm2, double &phi) |
| Computes Stansfield estimate of Maximum Likelihood solution of DF problem. | |
| void | computeMLFix (DFLib::Abstract::Point &MLFix) |
| Computes Maximum Likelihood solution of DF problem. | |
| void | aggressiveComputeMLFix (DFLib::Abstract::Point &MLFix) |
| more aggressive attempt to get at an ML fix | |
| void | computeCramerRaoBounds (DFLib::Abstract::Point &MLFix, double &am2, double &bm2, double &phi) |
| compute Cramer-Rao bounding ellipse parameters | |
| double | computeCostFunction (std::vector< double > &evaluationPoint) |
| compute cost function for point x,y | |
| void | computeCostFunctionAndGradient (std::vector< double > &evaluationPoint, double &f, std::vector< double > &gradf) |
| compute cost function for point x,y and its gradient | |
| void | computeCostFunctionAndHessian (std::vector< double > &evaluationPoint, double &f, std::vector< double > &gradf, std::vector< std::vector< double > > &h) |
| compute cost function for point x,y its gradient, and its hessian. | |
| int | numValidReports () const |
| virtual void | toggleValidity (int i) |
| bool | isValid (int i) const |
| int | size () const |
| const DFLib::Abstract::Report * | getReport (int i) const |
| int | getReportIndex (const std::string &name) const |
| return the index of the report that has the given name, or -1 | |
| int | getReportIndex (const DFLib::Abstract::Report *reportPtr) const |
| return the index of the report that has the given pointer, or -1 | |
| const std::vector< double > & | getReceiverLocationXY (int i) |
| virtual void | setEvaluationPoint (std::vector< double > &ep) |
| Set the point at which to evaluate the function. | |
| virtual double | getFunctionValue () |
| virtual double | getFunctionValueAndGradient (std::vector< double > &g) |
| virtual double | getFunctionValueAndHessian (std::vector< double > &g, std::vector< std::vector< double > > &h) |
 Public Member Functions inherited from DFLib::Abstract::Group Public Member Functions inherited from DFLib::Abstract::Group | |
| virtual | ~Group () |
| Provide a virtual destructor. | |
| virtual void | setEvaluationPoint (std::vector< double > &ep)=0 |
| Set the point at which to evaluate the function. | |
| virtual double | getFunctionValue ()=0 |
| virtual double | getFunctionValueAndGradient (std::vector< double > &gradient)=0 |
| virtual double | getFunctionValueAndHessian (std::vector< double > &gradient, std::vector< std::vector< double > > &hessian)=0 |
Private Member Functions | |
| ReportCollection (ReportCollection &right) | |
| ReportCollection & | operator= (ReportCollection &right) |
Private Attributes | |
| std::vector< DFLib::Abstract::Report * > | theReports |
| std::vector< double > | evaluationPoint |
| bool | f_is_valid |
| bool | g_is_valid |
| bool | h_is_valid |
| double | function_value |
| std::vector< double > | gradient |
| std::vector< std::vector< double > > | hessian |
Constructor & Destructor Documentation
◆ ReportCollection() [1/2]
|
private |
◆ ReportCollection() [2/2]
| DFLib::ReportCollection::ReportCollection | ( | ) |
◆ ~ReportCollection()
|
virtual |
DF Report Collection destructor.
Never destroys the objects in its vector, as they might be getting used for something else by caller
Member Function Documentation
◆ addReport()
|
virtual |
Add a DF report to the collection.
- Returns
- this report's number in the collection.

◆ aggressiveComputeMLFix()
| void DFLib::ReportCollection::aggressiveComputeMLFix | ( | DFLib::Abstract::Point & | MLFix | ) |
more aggressive attempt to get at an ML fix
compute ML fix
This is just a version of computeMLFix that tries a little harder to get at the answer.
The cost function is not guaranteed to have a unique minimum, and even when it does it is often hard to find. Originally, I used only the method of Conjugate Gradients to search for the minimum, but this fails rather often if the cost function has broad, flat areas of low value. The failure mode is that the line search in the steepest descent direction (the first step of the CG method) takes us very, very far away because rather than having a minimum in that direction, the function is simply asymptotic to some smallish value. Once it does this, the method can't recover because from there the function is completely flat.
So instead, before we try CG we do a Nelder-Mead downhill simplex search to improve our starting guess. So far, testing shows that this generally gets us very close to a minimum if there is one. Sometimes, though, it also goes off to infinity because the system simply doesn't have a clear minimum. In these cases it seems it is best for the user simply to ignore the fix. A more aggressive search for a constrained minimum (say the best point in some range of the starting point) could be a helpful thing, but is probably more work than this deserves.

◆ computeCostFunction()
| double DFLib::ReportCollection::computeCostFunction | ( | std::vector< double > & | evaluationPoint | ) |
compute cost function for point x,y
Compute Cost Function.
this returns the cost function for the transmitter being at x,y given the DF reports we have. The probability density uses the cost function in the argument of an exponential. Minimizing the cost function will therefore maximize the probability density.
The cost function is the sum 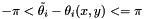
where 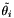
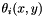
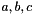
◆ computeCostFunctionAndGradient()
| void DFLib::ReportCollection::computeCostFunctionAndGradient | ( | std::vector< double > & | evaluationPoint, |
| double & | f, | ||
| std::vector< double > & | gradf | ||
| ) |
compute cost function for point x,y and its gradient

◆ computeCostFunctionAndHessian()
| void DFLib::ReportCollection::computeCostFunctionAndHessian | ( | std::vector< double > & | evaluationPoint, |
| double & | f, | ||
| std::vector< double > & | gradf, | ||
| std::vector< std::vector< double > > & | h | ||
| ) |
compute cost function for point x,y its gradient, and its hessian.

◆ computeCramerRaoBounds()
| void DFLib::ReportCollection::computeCramerRaoBounds | ( | DFLib::Abstract::Point & | MLFix, |
| double & | am2, | ||
| double & | bm2, | ||
| double & | phi | ||
| ) |
compute Cramer-Rao bounding ellipse parameters
Compute Cramer-Rao bounds.
This function returns the inverse squares and rotation angle for the 1-sigma Cramer-Rao bound of our probability distribution.
The Cramer-Rao theory states that the inverse of the Fisher information matrix is the best approximation to the covariance matrix obtainable from an unbiased estimator of the maximum likelihood.
This method simply computes the Fisher information matrix elements and computes from them the parameters of the ellipse.
If one compares the matrix elements of the FIM to the lambda, nu, and mu variables computed by the Stansfield estimator, one finds that they are equivalent if one makes the Stansfield approximation of small angles. Thus, this method provides precisely the same sort of error estimates for the Maximum Likelihood fix as the equivalent parameters returned by the Stansfield fix. They may be used in exactly the same manner to draw error ellipses around the ML fix.
The Fisher Information Matrix for the probability distribution associated with the ML fix is just:
![\[
I=\sum_i \frac{\left[
\begin{array}{cc}
(y_e-y_i)^2&-(x_e-x_i)(y_e-y_i)\\
-(x_e-x_i)(y_e-y_i)&(x_e-x_i)^2
\end{array} \right]}{\sigma_i^2[(x_e-x_i)^2+(y_e-y_i)^2]^2}
\]](form_56.png)
where 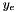
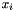
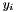
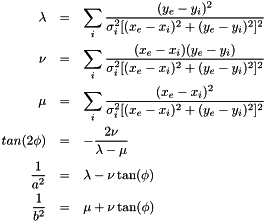
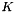
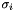
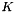
Thus, the correspondence with the Stansfield parameters is this:
![\begin{eqnarray*}
\lambda&=&\sum_i \frac{(y_e-y_i)^2}{\sigma_i^2[(x_e-x_i)^2+(y_e-y_i)^2]^2}\\
\nu&=&\sum_i \frac{(x_e-x_i)(y_e-y_i)}{\sigma_i^2[(x_e-x_i)^2+(y_e-y_i)^2]^2}\\
\mu&=&\sum_i \frac{(x_e-x_i)^2}{\sigma_i^2[(x_e-x_i)^2+(y_e-y_i)^2]^2}\\
tan(2\phi) &=& -\frac{2\nu}{\lambda-\mu}\\
\frac{1}{a^2}&=&\lambda - \nu\tan(\phi)\\
\frac{1}{b^2}&=&\mu + \nu\tan(\phi)
\end{eqnarray*}](form_61.png)


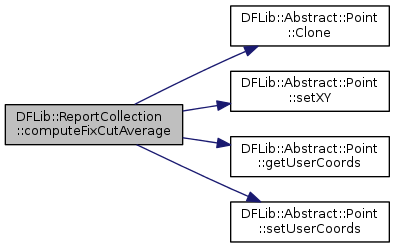
◆ computeFixCutAverage()
| bool DFLib::ReportCollection::computeFixCutAverage | ( | DFLib::Abstract::Point & | FCA, |
| std::vector< double > & | FCA_stddev, | ||
| double | minAngle = 0 |
||
| ) |
return the fix cut average of this collection's reports
A fix cut is the intersection of two DF reports. The Fix Cut Average is the average of all fix cuts from all pairs of reports in the collection. Fix cuts at shallow angles can be excluded by specifying a non-zero value for minAngle (in degrees).
- Parameters
-
FCA Returned fix cut average FCA_stddev standard deviation of fix cuts in user coordinates corresponding to the point provided in FCA minAngle reports whose fix cut occur at less than this angle will not be included in the average.

◆ computeLeastSquaresFix()
| void DFLib::ReportCollection::computeLeastSquaresFix | ( | DFLib::Abstract::Point & | LS_Fix | ) |
Computes least squares solution of DF problem.
compute least squares solution from all df reports.
The least squares solution is the point that has the minimum orthogonal distance to all bearing lines.
The least squares solution is given by
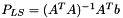
where 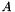
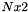
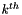
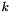
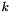
![$[\cos(\theta_k), -\sin(\theta_k)]$](form_7.png)
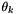
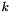
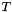
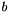
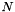
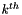
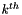
![$
b_k = [\cos(\theta_k),-sin(\theta_k)]\cdot[r_{kx},r_{ky}]
$](form_12.png)
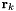
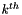
This method currently computes the matrix inverse 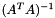
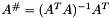

◆ computeMLFix()
| void DFLib::ReportCollection::computeMLFix | ( | DFLib::Abstract::Point & | MLFix | ) |
Computes Maximum Likelihood solution of DF problem.
compute ML fix
Given a collection of DF fixes with specified standard deviation, computes the point of maximum likelihood (ML fix).
The probability of a transmitter being at a particular location x,y given that each transmitter 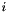
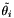
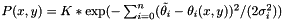
where 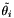
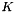
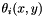
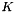
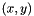
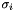
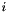
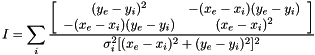
The ML fix is the point that minimizes the cost function, thereby maximizing the probability of that point.
To compute the ML fix requires an initial guess, as from the least squares fix. This method uses the method of Conjugate Gradients to find the minimum of the cost function. Note that it is sometimes (though rarely) the case in DF problems that the cost function is too flat near the minimum for conjugate gradients to converge. I have not characterized these pathological cases very well, but it does seem to be worst when the receivers are all off to one side of the transmitter. In these pathological cases, the first step of conjugate gradients shoots off to a very distant point where the function is almost completely flat, and never recovers. The only thing to do is to test the point returned by this method and make sure it is not unreasonably far from any receiver. I tend to use 100 miles as the test distance for a "ridiculous" solution.
If this method returns a ridiculous answer, one can try aggressiveComputeMLFix instead. That method uses a more robust—but possibly less efficient—minimization method as a first step to refine the initial guess to conjugate gradients.


◆ computeStansfieldFix()
| void DFLib::ReportCollection::computeStansfieldFix | ( | DFLib::Abstract::Point & | SFix, |
| double & | am2, | ||
| double & | bm2, | ||
| double & | phi | ||
| ) |
Computes Stansfield estimate of Maximum Likelihood solution of DF problem.
Compute Stansfield fix.
Given a collection of DF fixes with specified standard deviation, computes the point of maximum likelihood in the approximation of small angles. It is based on the paper "Statistical Theory of D.F. Fixing" by R. G. Stansfield, J. I.E.E. Vol 94, Part IIA, 1947. Unfortunately, this paper is not available anywhere on the web, and it is hard to find it even in well stocked technical libraries. I was able to obtain a copy through IEEE Document Search, but paid through the nose for it — and due to copyright issues I am not permitted to make copies available. If you wish to obtain this paper, you'll have to get a copy yourself. A more easily obtained paper is "Airborne Direction Finding---The Theory of Navigation Errors" by C.J. Ancker in IRE Transactions on Aeronautical and Navigational Electronics, pp 199-210 (1958). While paper is this paper available in PDF format through IEEE Xplore at http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4201630&tag=1 it is unfortunately accessible only to those who have access through a library or IEEE membership. Ancker's paper is much more readable than Stansfield's, as he uses a somewhat less opaque notation and is much more explicit about the approximations being made.
Since it is so difficult to obtain primary sources describing the Stansfield estimator, I'll present the theory in full.
Stansfield's approach approximates the bearing error 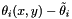
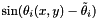
Fly in the ointment: Stansfield uses angles measured counter-clockwise from the East in those equations. To keep consistent with Stansfield's paper, I retain his convention throughout this documentation. Do remember when reading DFLib code that we use a different convention, and therefore the code does not exactly match the theoretical exposition. To translate from Stansfield's to our usage (bearings clockwise from North) simply interchange cosine and sine in the final expressions below.
Starting as in the Maximum Likelihood fix, we assume that the probability of the true bearing from any given receiver to the actual target location being 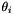
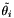
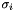
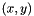
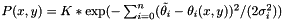
In this expression, 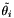
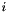
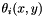
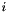
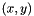
Making the substitution of small angular error, 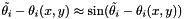
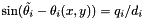
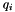
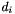
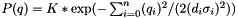
Unfortunately, the 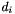
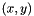
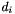
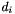
Assume that 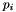
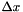
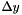
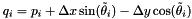
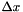
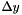
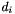
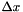
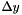
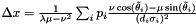
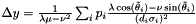
with 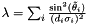
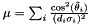
and 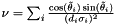
Finally, it is the case that the numbers 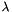
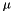
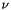
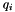
If one rotates the system of coordinates around the maximum likelihood fix location by an angle 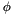
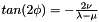
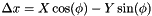
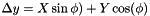
where the delta quantities are offsets from the fix location, then the region defined by:
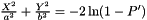
encloses the region in which there is a probability 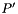
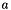
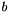
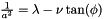
and
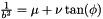
Note that Stansfield's paper has an error in it regarding the two expressions above. The error was pointed out and corrected in a report "Probabalistic Position-Fixing" by Steve Burnett et al. This paper was a report from the Claremont Graduate School, Claremont McKenna College Mathematics Clinic, 1986. The only place I've been able to find it is the URL:
http://oai.dtic.mil/oai/oai?verb=getRecord&metadataPrefix=html&identifier=ADA190397
Remember when reading the code that Stansfield uses a different angle convention for bearings than DFLib does.
And there is another subtlety that is not discussed in Stansfield, but is discussed in "Numerical Calculations for Passive Geolocation Scenarios" by Don Koks
http://www.dsto.defence.gov.au/publications/4949/DSTO-RR-0319.pdf
Since the Stansfield fix is supposed to be a solution to the minimization of the cost function (and therefore the maximization of the probability density), the presence of the distance from receiver to test point in the cost function is a problem that interferes with the solution. To get the closed-form solution, we have to assume that the 
0) starting with an initial guess point O, compute the distances from receivers to O, call them 
Iterate:
1) Using the 
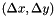
2) Compute the distances from receivers to 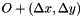
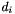
3) If 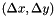
The "changed appreciably" bit will take a little black art, I think. I propose that we simply check that the norm of the offset vector hasn't changed more than some tolerance since the last iteration.

◆ deleteReports()
|
virtual |
destroy all reports stored in collection
Provided in case our caller does NOT need the stored pointers for something else, and doesn't want to keep track of them.
◆ getFunctionValue()
|
inlinevirtual |
- Returns
- function value
Implements DFLib::Abstract::Group.
◆ getFunctionValueAndGradient()
|
inlinevirtual |
◆ getFunctionValueAndHessian()
|
inlinevirtual |
- Parameters
-
g gradient returned h hessian returned
- Returns
- function value
Implements DFLib::Abstract::Group.
◆ getReceiverLocationXY()
|
inline |
◆ getReport()
|
inline |
◆ getReportIndex() [1/2]
| int DFLib::ReportCollection::getReportIndex | ( | const DFLib::Abstract::Report * | reportPtr | ) | const |
return the index of the report that has the given pointer, or -1
Stupid linear search, but should be OK for a realistic size of collection.
◆ getReportIndex() [2/2]
| int DFLib::ReportCollection::getReportIndex | ( | const std::string & | name | ) | const |
return the index of the report that has the given name, or -1
Stupid linear search, but should be OK for a realistic size of collection.
◆ isValid()
|
inline |

◆ numValidReports()
| int DFLib::ReportCollection::numValidReports | ( | ) | const |

◆ operator=()
|
private |
◆ setEvaluationPoint()
|
inlinevirtual |
Set the point at which to evaluate the function.
Implements DFLib::Abstract::Group.
◆ size()
|
inline |
◆ toggleValidity()
|
inlinevirtual |
Member Data Documentation
◆ evaluationPoint
|
private |
◆ f_is_valid
|
private |
◆ function_value
|
private |
◆ g_is_valid
|
private |
◆ gradient
|
private |
◆ h_is_valid
|
private |
◆ hessian
|
private |
◆ theReports
|
private |
The documentation for this class was generated from the following files:
- /users/russo/DFLIB_Git/DFLib/DF_Report_Collection.hpp
- /users/russo/DFLIB_Git/DFLib/DF_Report_Collection.cpp